Annuity

The concept of the Time Value of Money recognizes that a sum of money today is worth more than the same sum in the future due to its potential earning capacity. This is fundamentally linked to the idea of interest and the process of compounding or discounting. Within this framework, we can determine the Future Value (FV), which is the value at some future time of a present amount or a series of payments, evaluated at a given interest rate, and the Present Value (PV), which is the current value of a future amount or a series of payments, evaluated at a given interest rate.

A key concept within the time value of money, particularly concerning a series of payments, is the Annuity. An annuity is defined as a series of periodic cash flows (payments or receipts) of equal amounts. These payments occur over a specified number of periods. Examples include the premium payment of a life insurance policy or annual deposits into a sinking fund. The time period between two successive payments is called the payment period. While commonly referred to in the context of annual payments, the term “annuity” in a broader sense includes payments that can be annual, semi-annual, quarterly, or other lengths of time.

Annuities can be classified based on the timing of the cash flows within each period:

• Ordinary Annuity (or Regular Annuity or Deferred Annuity): Cash flows occur at the end of each period.
• Annuity Due: Cash flows occur at the beginning of each period.

The provided sources primarily focus on the ordinary annuity for calculations. We can calculate both the future value and the present value of an annuity.

Future Value of an Ordinary Annuity

The future value of an ordinary annuity is the sum of the compound amounts of all the periodic payments at the end of the annuity’s duration. Essentially, it’s how much a series of regular, equal deposits will grow to over time, assuming a specific interest rate is earned on the accumulated balance. This value is determined through the process of Compounding.

The formula for the future value (FVAn or Sn) of an ordinary annuity is given as: FVAn = A [ {(1+r)ⁿ – 1} / r ] or Sn = R [((1+i)ⁿ – 1)/i]

Where:

• FVAn or Sn = Future value of the annuity at the end of ‘n’ periods.
• A or R = The constant amount of each periodic payment or installment.
• r or i = The interest rate per period.
• n = The number of periods or the duration of the annuity.

The term [{(1+r)ⁿ – 1} / r] or [((1+i)ⁿ – 1)/i] is known as the future value interest factor of an annuity (FVIFA r,n or FVIFA(i,n)). Tables are available that provide these factors for various combinations of interest rates and periods. The future value of the annuity can thus be calculated by multiplying the periodic payment by the appropriate FVIFA from the table.

Let’s look at some examples from the sources:

• Suppose you deposit ₹1,000 annually in a bank for 5 years, and these deposits earn a compound interest rate of 10%. Assuming each deposit occurs at the end of the year (ordinary annuity), the future value at the end of 5 years is calculated using the formula: FVAn = 1000 * [{(1+0.10)⁵ – 1} / 0.10] FVAn = 1000 * [{(1.1)⁵ – 1} / 0.1] FVAn = 1000 * [{1.61051 – 1} / 0.1] (Note: Source calculation shows 1.6105, resulting in 0.6105/0.1 = 6.105) FVAn = 1000 * [0.61051 / 0.1] FVAn = 1000 * 6.1051 The future value is ₹6,105.10. Source rounds this to ₹6,105. Using the FVIFA table, the FVIFA for 5 periods at 10% is 6.105. So, 1000 * 6.105 = ₹6,105.
• Mr. X is depositing ₹20,000 annually in a recurring bank deposit paying 9% compounded interest. To find out how much Mr. X will get at the end of the 5th year, we use the future value of annuity formula: FVAn = A[{(1+r)ⁿ-1}/r] FVAn = ₹20,000 * 1 [{(1+0.09)⁵-1}/0.09] FVAn = ₹1,19,694.
• A person is required to pay annual payments of ₹8,000 into a Deposit Account that pays 10% interest per year. The future value of this annuity at the end of 5 years is calculated as: FVAn = A[{(1+r)ⁿ-1}/r] FVAn = ₹8,000 * [((1+0.10)5 -1)/0.10] FVAn = ₹8,000 * 6.1051 The future value is ₹48,841.
• The future value of an annuity of ₹100 for 10 years at 10% interest is calculated using the FVIFA: Future Value of Annuity = A × FVIFA i,n Future Value of Annuity = ₹100 × 15.937 (The FVIFA 10%, 10 is 15.937, although not explicitly shown in the truncated table snippets provided, this factor would be found in a full FVIFA table) The future value is ₹1,593.7.

Applications of the future value of an annuity include knowing the accumulated fund at a certain period (like deposits in a Public Provident Fund) or determining how much a person should save annually to accumulate a target amount in the future (like annual savings to buy a house or deposits in a sinking fund). For example, Apex Ltd. needs to accumulate ₹50 crore in 6 years in a sinking fund earning 12% interest. To find the required annual deposit, the future value formula is used in reverse: A = FVAn / FVIFAn,r The FVIFA for 6 years at 12% is 8.115. Annual Deposit = ₹5,00,00,000 / 8.115 = ₹61,61,429.00.

Present Value of an Ordinary Annuity

The present value of an ordinary annuity is the sum of the present values of all the periodic cash flows, discounted back to the present point in time. The process of finding the present value is called Discounting, and it is the reverse of compounding. The present value represents the lump sum amount today that is equivalent in value to the series of future equal payments, given a specific discount rate.

The formula for the present value (PVAn or S) of an ordinary annuity can be expressed in several equivalent forms: PVAn = A [{1 – (1/1+ r) n}/r] S = A [ 1-(1+ i)⁻ⁿ / i ] PVAn = A [ (1+𝑘)^𝑛−1 / 𝑘(1+𝑘) ] (This form uses the FVIFA factor in the numerator and discounts it) Or, more commonly derived from the future value formula: PVAn = A * [{1 – (1+r)⁻ⁿ} / r]

Where:

• PVAn or S = Present value of the annuity.
• A or R = The constant amount of each periodic payment or installment.
• r or i or k = The discount rate per period.
• n = The number of periods or the duration of the annuity.

The term [{1 – (1/1+ r) ⁿ}/r], [ 1-(1+ i)⁻ⁿ / i ], or [ (1+𝑘)^𝑛−1 / 𝑘(1+𝑘) ] is known as the present value interest factor of an ordinary annuity (PVIFAr,n or PVIFA(i,n)). Tables are available for these factors. The present value of the annuity can be found by multiplying the periodic payment by the appropriate PVIFA from the table.

Examples from the sources illustrate the calculation:

• Suppose you expect to receive ₹1,000 annually for 3 years, with each receipt occurring at the end of the year. If the discount rate is 10%, the present value is the sum of the present values of each individual inflow: Year 1 PV = ₹1,000 × (1/1.10) = ₹1,000 × 0.9091 = ₹909.10 Year 2 PV = ₹1,000 × (1/1.10)² = ₹1,000 × 0.8264 = ₹826.40 Year 3 PV = ₹1,000 × (1/1.10)³ = ₹1,000 × 0.7513 = ₹751.30 Total Present Value = ₹909.10 + ₹826.40 + ₹751.30 = ₹2,486.80. Source calculation gives ₹2,486.70 due to minor rounding difference in factors. Using the formula S = A [ 1-(1+ i)⁻ⁿ / i ]: S = ₹1,000 [ 1 – (1+0.10)⁻³ / 0.10 ] = ₹1,000 [ 1 – (1/1.10)³ / 0.10 ] S = ₹1,000 [ 1 – 0.7513 / 0.10 ] = ₹1,000 [ 0.2487 / 0.10 ] = ₹1,000 * 2.487 S = ₹2,487 (again, minor difference from summing individual PVs due to rounding of factors).
• To find the present value of a 4-year annuity of ₹10,000 discounted at 10%: PVAn = A [ (1+𝑘)^𝑛−1 / 𝑘(1+𝑘) ] PVAn = ₹10,000 * [ (1+.10)⁴⁻¹ / .10(1+.10)⁴ ] PVAn = ₹10,000 * [ (1.4641)⁻¹ / .10(1.4641) ] PVAn = ₹10,000 * [ 0.4641 / 0.14641 ] PVAn = ₹10,000 * 3.17008 The present value is ₹31,700. Using the PVIFA table, the PVIFA for 4 periods at 10% is 3.170. 10,000 * 3.170 = ₹31,700.
• If an investor wants to receive five annual payments of ₹10,000 starting at the end of this year and the bank offers 10% interest, the amount they should invest now (the present value of the annuity) is needed. Using the PVIFA table, the PVIFA for 5 periods at 10% is 3.791 (This is not shown in the provided snippet but is the correct factor). The present value is ₹10,000 * 3.791 = ₹37,910.

The present value of an annuity can be applied in cases like loan amortisation by a borrower. It is also used in bond valuation, where the periodic interest payments (coupon payments) can be treated as an annuity, and their present value is calculated using the PVIFA formula.

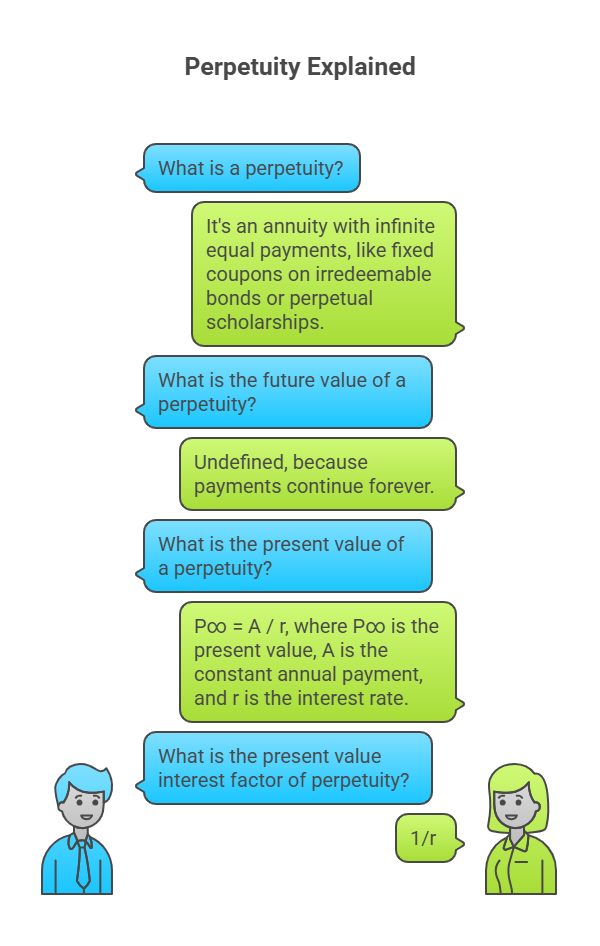
Perpetuity: A Special Case of Annuity

A perpetuity is a type of annuity where the series of equal payments or receipts continues indefinitely, meaning the cash flows continue for an infinite amount of time. Examples include fixed coupon payments on permanently invested (irredeemable) bonds or perpetual scholarships from an endowment fund.

Since the payments continue forever, the future value of a perpetuity is undefined. However, the present value of a perpetuity is finite. As the number of periods ‘n’ approaches infinity, the term (1+r)⁻ⁿ in the present value of annuity formula approaches zero. Thus, the formula for the present value of a perpetuity (P∞) simplifies: P∞ = A / r

Where:

• P∞ = Present value of the perpetuity.
• A = The constant annual payment.
• r = The interest rate (or discount rate) per period, expressed in decimal form.

The present value interest factor of perpetuity (PVIF Ar,∞) is simply 1 divided by the interest rate (1/r).

In summary, understanding the value of an annuity, whether its future value determined through compounding or its present value determined through discounting, is essential in financial management. These calculations allow for the evaluation of a series of equal cash flows over time, using specific formulas and interest factors provided in tables based on the period and interest rate.