The Future Value (FV) is a core dimension of the Time Value of Money. It is defined as the value at some future time of a present amount of money, or a series of payments, evaluated at a given interest rate. The concept of Future Value is closely associated with Compounding, which is the process of determining the future value of cash flows by calculating the effect of earning interest on interest over time. We determine Future Values (FV) of all cash flows at the end of a specified time period using a given interest rate. This contrasts with Present Value, which is determined through Discounting, the reverse process of compounding used to find the current value of future cash flows.
Future Value calculations can be applied to different patterns of cash flows:
- A Single Flow.
- Multiple Flows (which may be uneven).
- An Annuity (a series of equal payments).
Future Value of a Single Cash Flow
The future value of a single cash flow is the amount that a single deposit made today will grow to at some future date, assuming a specific interest rate is earned over the investment period.
The general formula for the future value (FV or S) of a single present amount (PV or P) invested for ‘n’ periods at an interest rate ‘r’ or ‘i’ per period is: FV = PV * (1+r)n or S = p * (1+i)n or FV = PV * FVIFr,n
Here:
- FV or S = Future value ‘n’ years hence.
- PV or p = Present Value or Amount invested today.
- r or i = Interest rate per period.
- n = Number of periods of investments or number of years.
- FVIFr,n = Future Value Interest Factor for a single sum.
The term (1+r)n is known as the compounding factor or the future value interest factor (FVIFr,n or FVIF(i,n)). Tables are available that provide the value of FVIF for various combinations of interest rates (i) and periods (n).
Examples from the sources illustrate the calculation of future value for a single amount:
- Suppose you have ₹1,000 today and deposit it with a financial institution that pays 10% interest compounded annually for 3 years. The deposit grows as follows:
- End of Year 1: Principal ₹1,000 + Interest (1,000 * 0.10) ₹100 = ₹1,100.
- End of Year 2: Principal ₹1,100 + Interest (1,100 * 0.10) ₹110 = ₹1,210.
- End of Year 3: Principal ₹1,210 + Interest (1,210 * 0.10) ₹121 = ₹1,331. Using the formula: FV = 1000 * (1 + 0.10)3 = 1000 * (1.331) = ₹1,331.
- The future value of ₹1000 at the end of 1 year at 7% interest is calculated as 1000 * (1+7/100)1 = 1000 * 1.07 = ₹1070.
- For a 3-year deposit of ₹1000 at 7% interest, the future value is 1000 * (1+7/100)3 = 1000 * (1.07)3 = 1000 * 1.22 = ₹1220.
- If a person invests ₹1,50,000 at 12% interest, the future value at the end of 10 years is 1,50,000 * (1 + 0.12)10 = 1,50,000 * 3.106 = ₹4,65,900.
- The future value of an initial ₹100 compounded annually for 10 years at 10% is 100 * (1+0.10)10 = 100 * 2.5937 = ₹259.4.
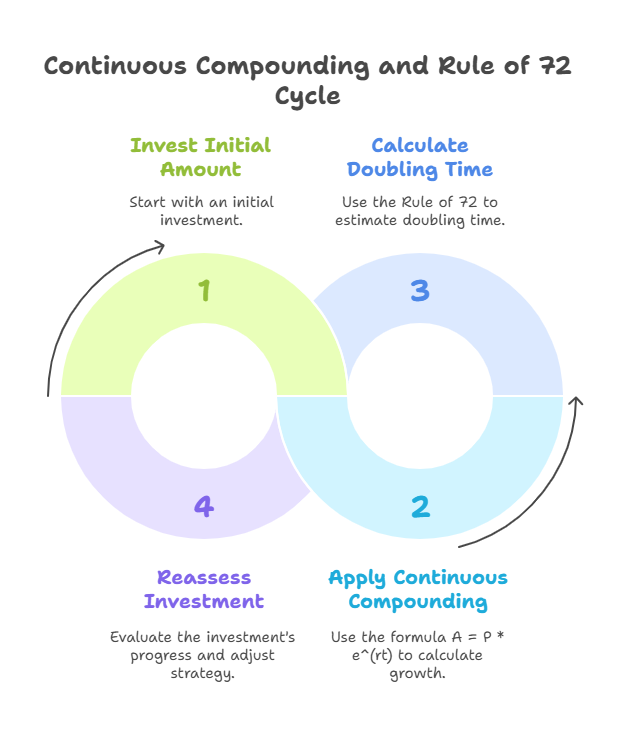
For cases where compounding occurs multiple times within a year, say ‘m’ times, the formula can be adjusted. However, specific formulas for compounding multiple times are not fully detailed for single flows in the provided text beyond mentioning m. The concept of continuous compounding is mentioned, particularly in the context of derivatives. The formula for the terminal value (A) of an amount (P) invested at a continuously compounded rate of interest (r) for (t) years is given as A = P * e(rt), where ‘e’ is the exponential constant.
An approximation for the time it takes for an amount to double at a given compound rate is the Rule of 72. You divide 72 by the rate of interest to get an approximate number of years for the investment to double. For example, at a compound rate of 12% per year, it takes approximately 72 / 12 = 6 years to double ₹5,000.
Future Value of Multiple Uneven Flows
If you have a series of cash flows of different amounts occurring over different periods, their future value is the sum of the future values of each individual cash flow compounded to the end of the final period. The formula is FV = PV1 * (1+r)n + PV2 * (1+r)n-1 + … + PVn * (1+r)1 or more generally, FV = Σ At * (1+r)(n-t) where At is the cash flow at time t.
Future Value of an Annuity
An annuity is a series of equal payments or receipts occurring over a specified number of periods. If the cash flows occur at the end of each period, it’s called an ordinary annuity or regular annuity. If they occur at the beginning of each period, it’s called an annuity due. The sources primarily focus on the ordinary annuity.
The future value (FVAn or Sn) of an ordinary annuity where a constant periodic flow (A or R) is received or paid for ‘n’ periods at an interest rate ‘r’ or ‘i’ per period is given by the formula: FVAn = A * [{(1+r)n – 1} / r] or Sn = R * [((1+i)n – 1)/i]
Here:
- FVAn or Sn = Future value of the annuity which is the sum of the compound amounts of all payments and a duration of n periods.
- A or R = Amount of each instalment or constant periodic flow.
- r or i = Interest rate per period.
- n = Number of periods or duration.
The term [{(1+r)n – 1} / r] or similar variations is known as the future value interest factor of an annuity (FVIFAr,n or FVIFA(i,n)). Tables for FVIFA(i,n) are available.
Examples from the sources illustrate the calculation of future value for an annuity:
- Suppose you deposit ₹1000 annually in a bank for 5 years at a compound interest rate of 10%. Assuming deposits occur at the end of the year (ordinary annuity), the future value will be:
- Using the formula: 1000 * [{(1.1)5 – 1} / 0.1] = 1000 * [{1.61051 – 1} / 0.1] = 1000 * [0.61051 / 0.1] = 1000 * 6.1051 = ₹6105.1. Note: The provided source calculation shows a slight discrepancy 1.6105-1= .615/.1= 6.105*1000= 6105. Another example uses ₹8,000 per period for 5 years at 10%, resulting in 8000 * 6.1051 = ₹48,841.
- Using a future value interest factor table: The FVIFA for 5 years at 10% is 6.105. So, ₹1000 * 6.105 = ₹6105.
- Apex Ltd. needs to accumulate ₹50 crore in 6 years and deposits annually into a sinking fund earning 12% interest. To find the annual deposit amount, you would use the future value of an annuity formula, rearranging to solve for A: A = FVAn / FVIFA(r,n). The FVIFA for 6 years at 12% would be needed from a table or calculated.
In summary, Future Value is the value of money at a point in the future, calculated by compounding current or periodic cash flows at a given interest rate. It is a crucial tool in financial management for understanding how investments grow over time.