The Time Preference for Money, also referred to as the Time Value of Money, is a fundamental concept in Financial Management. It explains that a unit of money received today is worth more than a unit of money received in the future. This phenomenon arises because money received now and money received in a future period cannot have the same worth.
Most financial decisions, whether personal or business, involve considerations of the time value of money. Financial problems often involve cash flows that occur at different points in time, and evaluating these cash flows explicitly requires considering the time value of money. Benefits or costs, regardless of their form (profit or cash flow), that belong to two different time periods are not additive unless they are converted into a similar measure, either future value or present value. Non-discounted cash flow methods, such as the Accounting Rate of Return (ARR) or Payback Period, do not take the time value of money into consideration and may, as a result, often mislead the decision maker.
Several reasons contribute to an individual’s preference for possessing a given amount of money now rather than receiving the same amount at a later date:
- Risk: There is inherent uncertainty about receiving future cash flows. A rupee received today is certain, whereas a rupee receivable tomorrow is less certain, embodying the “bird-in-the-hand” principle in investment decisions. Furthermore, during a period of inflation, a rupee today possesses greater real Purchasing Power compared to a rupee received a year hence. This purchasing power risk contributes to the preference for receiving cash sooner.
- Preference for Consumption: Individuals generally tend to prefer current consumption over delaying it to the future. The immediate gratification of consumption is often preferred.
- Investment Opportunities: Money received today can be productively employed to generate positive returns. An investment of one rupee today could grow to (1+r) in a year, where ‘r’ is the rate of return earned on the investments. For example, if the risk-free rate of return is 12%, an individual would be indifferent between receiving 1000 now or1120 in one year’s time. This is because the present value of 1120 receivable one year hence is1000, calculated using a 12% discount rate. Conversely, 1,000 received twelve months from now, discounted at a rate of 10%, would be worth approximately909 today. This opportunity cost of funds is a direct consequence of the time value of money. The discount rate selection for cash flows is an important aspect in financial management.
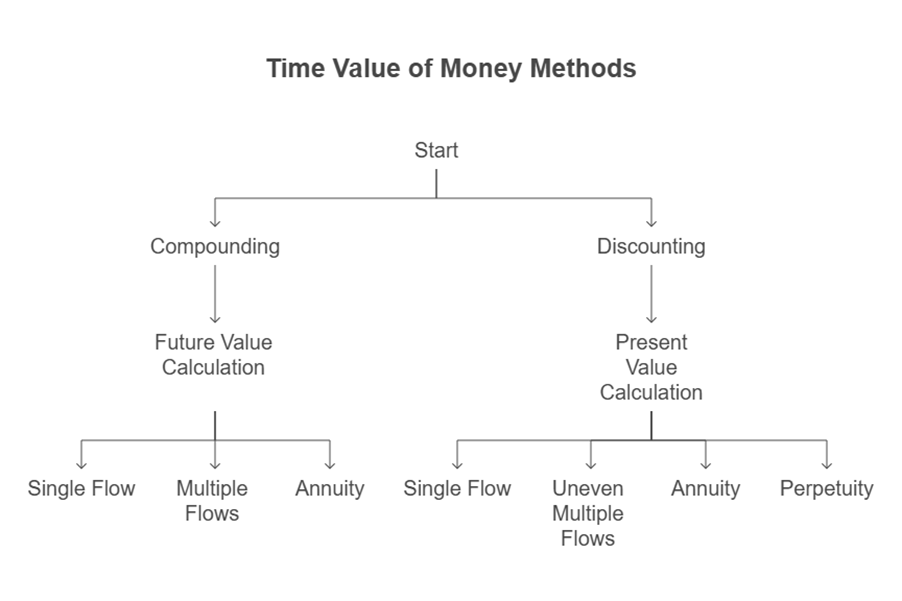
There are two primary methods or techniques for estimating the time value of money:
- Compounding (Future Value): This method is used to determine the value at some future point in time of a present amount of money or a series of payments. This value is calculated based on a given interest rate. Compounding essentially calculates how an investment grows over time by earning interest on both the initial principal and the accumulated interest from previous periods.
- For a single flow, the future value grows over time, as illustrated by depositing `1,000 at 10% compounded annually.
- The calculation for future value in the case of simple interest is the principal amount (P0) plus the simple interest (SI), where SI is calculated as P0 multiplied by the interest rate (i) and the number of periods (n). Future value can be applied to a single flow, multiple flows, or an annuity. Complex calculations, like ascertaining the future value of 70,000 at 8% computed semi-annually for 5 years or the compound interest on60,000 at 6% computed semi-annually for 5 years, involve compounding. Investment evaluations might compare future values based on different compounding frequencies, such as continuous compounding versus monthly compounding.
- Discounting (Present Value): This method calculates the current value (the value at time “O”) of a future amount of money or a series of cash flows. This calculation is performed using a given interest rate, known as the discount rate. Discounting involves comparing an initial outflow with the sum of the present values of future inflows, evaluated at the specified interest rate. The present value represents the amount that would need to be invested today, at the given interest rate, to accumulate to the future amount.
- The concept of the present value of cash flows is fundamental. It recognizes that cash flow streams occurring at different time periods have different values and can only be compared when they are expressed in terms of a common denominator – their present values. Discounting thus explicitly takes into account the time value of money.
- Discounting can be applied to a single flow, uneven multiple flows, an annuity, or a perpetuity. The present value interest factor for an annuity is [{1- (1/1+r)n}/r], where ‘r’ is the discount rate and ‘n’ is the number of periods.
- A perpetuity is a specific type of annuity where the stream of cash flows continues indefinitely. Despite the infinite duration of the cash flows, the value of a perpetuity is finite. This is because cash flows expected far into the future have extremely low present values when discounted. Examples of perpetuities include fixed coupon payments on permanently invested (irredeemable) sums of money or perpetual scholarships paid from an endowment fund. For academic knowledge, the cost of irredeemable preference shares (though not allowed as per Companies Act, 2013) can be calculated using a perpetuity formula.
- The concept of present value is essential for applying discounted cash flow techniques.
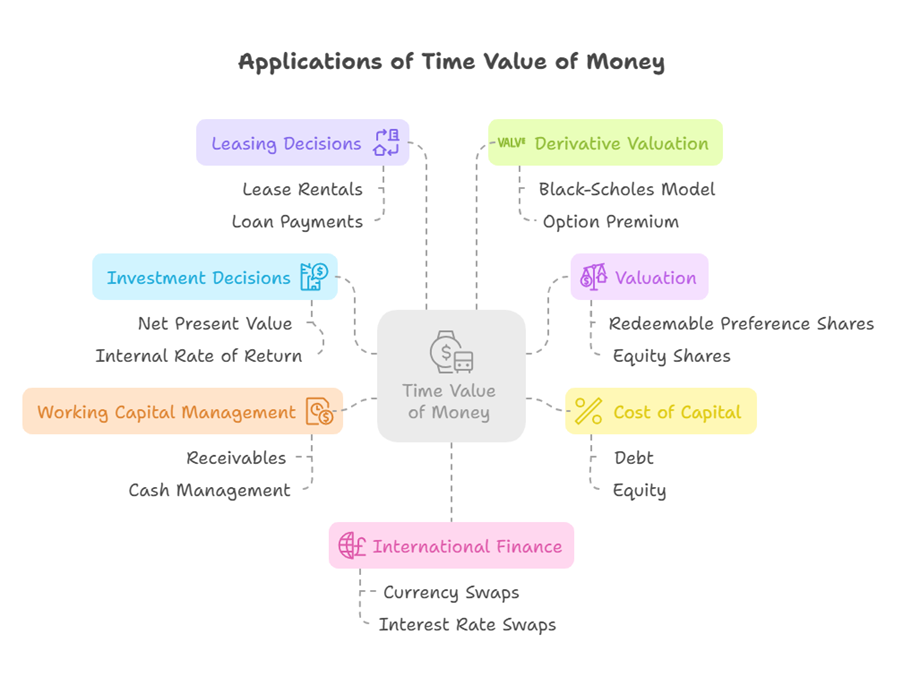
The time value of money is a critical concept applied in various areas of financial management:
- Investment Decisions (Capital Budgeting): This is a core area where TVM is applied. Evaluating investment projects involves comparing the initial investment (a present cash flow) with the future cash flows generated by the project. Discounted cash flow techniques like Net Present Value (NPV), Internal Rate of Return (IRR), Profitability Index (PI), and Discounted Payback Period explicitly incorporate the time value of money by discounting future cash flows to their present value. The IRR is the discount rate at which the present value of future cash flows equals the initial investment, resulting in a zero NPV. The cost of capital is typically used as the discount rate (k) in these analyses. Projects are often evaluated based on after-tax incremental cash flows, considering aspects like depreciation and working capital, to determine the actual cash flows that need to be discounted.
- Valuation: The valuation of financial instruments and assets heavily relies on TVM. The value of redeemable preference shares, for instance, is calculated as the present value of all expected future dividend payments and the maturity value, discounted at the required rate of return. Similarly, the cost of redeemable preference share capital is derived from a formula that equates the net proceeds from the issue to the present value of future dividends and redemption value. Valuation of equity shares, debentures, and bonds also involves discounting expected future cash flows (dividends, interest, principal repayment) to their present value. The value of a perpetuity is finite because future cash flows are discounted. Terminal Value calculations for valuation beyond a forecast period also use discounted cash flow formulas.
- Cost of Capital: The cost of capital for different sources of finance (debt, preference shares, equity) is a key input (the discount rate) for investment decisions and valuation, and its calculation often involves TVM. The cost of preference share capital, for example, is the rate that discounts the future preference dividends and redemption value back to the issue price. Opportunity cost, a crucial element of the rationale for TVM, is considered an implicit cost of capital like retained earnings.
- Working Capital Management: While focused on short-term assets and liabilities, managing working capital involves timing of cash flows. Concepts like the opportunity cost of funds tied up in receivables are direct applications of TVM. Evaluating credit policies involves assessing the trade-off between increased sales/profit and the opportunity cost of maintaining higher receivables. Cash management aims to use excess cash profitably, implying earning a return on it over time, which involves TVM. Short-term money market instruments like commercial paper are often issued at a discount and redeemed at face value, with the difference reflecting the time value of money over their short maturity period.
- Leasing Decisions: Evaluating whether to lease or buy an asset involves comparing the present value of cash flows under each option, including lease rentals, loan payments, interest, depreciation tax shields, etc., discounted at an appropriate rate.
- Derivative Valuation: The valuation of financial derivatives, particularly options, incorporates the time value of money. The premium of an option is influenced by factors including the time to expiry and interest rates. Option pricing models like Black-Scholes explicitly use the risk-free rate to discount future values (like the exercise price) back to the present. The “time value” of an option is the portion of its premium exceeding its intrinsic value.
- International Finance: Decisions involving foreign currencies and interest rates over time, such as evaluating projects in foreign countries or using instruments like currency swaps or interest rate swaps, necessitate the application of TVM principles. Comparing cash flows in different currencies at different points in time requires discounting.
In summary, the time preference for money is a core principle in finance acknowledging that money has a higher value the sooner it is received due to factors like risk, consumption preference, and investment opportunities. This principle is quantified using techniques like compounding (for future value) and discounting (for present value), which are essential for evaluating cash flows occurring at different times across various financial decisions, including investment appraisal, financing, valuation, and working capital management. Non-discounted methods, by neglecting this principle, can lead to suboptimal decisions.